SAT Geometry and Trigonometry – Hack Points and Practice Questions
The SAT exam has around 5 to 7 SAT Geometry and Trigonometry content domain questions out of 44 SAT Math questions. This makes up around 15% of the SAT Math. Note that, SAT Geometry and Trigonometry is the content domain where many SAT exam students wobble. Having a solid SAT Geometry and Trigonometry background and solving as many SAT Geometry and Trigonometry Practice questions as possible is key to having a high SAT Math score.
In this article
📌 Hint: Do not skip this article, you will find FREE SAT Math Prep resources throughout the article.
We’ve listed the most important and frequently occurring concepts in this SAT Geometry and Trigonometry post. You will see SAT Geometry and Trigonometry practice test questions and exercises, in total 8 Geometry and Trigonometry questions with rationales all for FREE.
💡You might be interested in reading the Digital SAT Math Prep post.
SAT Geometry and Trigonometry Content Domain
Geometry is the study of different shapes, sizes, and positions of different shapes based on the number of sides, angles, and so on. Whereas trigonometry is the subset of geometry that deals with the properties of one of the shapes in geometry called “triangle”. In the SAT Geometry and Trigonometry domain, the College Board assesses the abilities of students in solving problems that focus on area and volume; angles, triangles, trigonometry; and circles.
💡You might be interested in reading the Digital SAT Math Ultimate Guide post. We have provided further details about the SAT Math structure, examples of easy, medium, and hard questions, answers, rationales, and frequently asked questions about the SAT Math.
Anna B. Scored 800 on SAT Math!
Anna B. is one of our thousands of successful SAT students. She scored 800 on SAT Math. You can watch her SAT story.
SAT Geometry and Trigonometry Skills and Knowledge Testing Points
Geometry and Trigonometry is the fourth and last content domain in SAT Math. The SAT exam will have around 5 to 7 questions from the Geometry and Trigonometry content domain. There are 4 skills and knowledge testing points in the SAT Geometry and Trigonometry content domain:
-
- Area and Volume
- Lines, angles, and triangles
- Right triangles and trigonometry
- Circles
👉 Take our full-length FREE SAT Practice Test, see where you stand!
Let’s review the important points you should know for each of the SAT Geometry and Trigonometry skills and knowledge below.
🗎 Download the 15-page Digital SAT Math Formula Sheet.
SAT Geometry Topic 1: Area and Volume – Important Points
Area measures the amount of space inside a two-dimensional shape, while volume measures the space a three-dimensional object occupies. Both concepts are fundamental in SAT geometry and have numerous real-world applications, such as calculating the amount of paint needed to cover a wall or the volume of water a container can hold.
Calculating Area of Basic Shapes
Rectangles and Squares:
- Formula for Rectangle: Area = Length . Width
- Formula for Square: Area =

Triangles:
- Formula: Area =

Parallelograms:
- Formula: Area = Base . Height
Trapezoids:
- Formula: Area =

Circles:
- Formula: Area =

Memorize these formulas for solving SAT Geometry questions correctly.
Calculating Volume of Basic Solids
Cubes and Rectangular Prisms:
Formula for Cube: 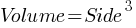
Formula for Rectangular Prism: Volume = Length . Width . Height
Cylinders:
Formula: Volume= 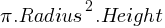
Cones:
Formula: Volume =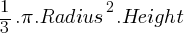
Spheres:
Formula: Volume = 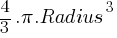
Composite Shapes and Solids
For composite shapes, break them down into simpler shapes, calculate the area or volume of each part, and then add them together.
Example: To find the area of a shape made from a rectangle and a semicircle:
- Calculate the area of the rectangle.
- Calculate the area of the semicircle.
- Add the two areas together.
Surface Area of Solids
Surface Area of Cubes and Rectangular Prisms:
- Cube: Surface Area =

- Rectangular Prism: Surface Area = 2lw + 2lh + 2wh
Cylinders:
- Formula: Surface Area=
 (top and bottom circles + lateral area)
(top and bottom circles + lateral area)
Cones:
- Formula: Surface Area =
 (base area + lateral area, where l is the slant height)
(base area + lateral area, where l is the slant height)
Spheres:
- Formula: Surface Area =

Note that, some of these formulas are provided on the SAT exam as follows. However, memorizing them will save you time when solving SAT Geometry problems in the SAT Exam.
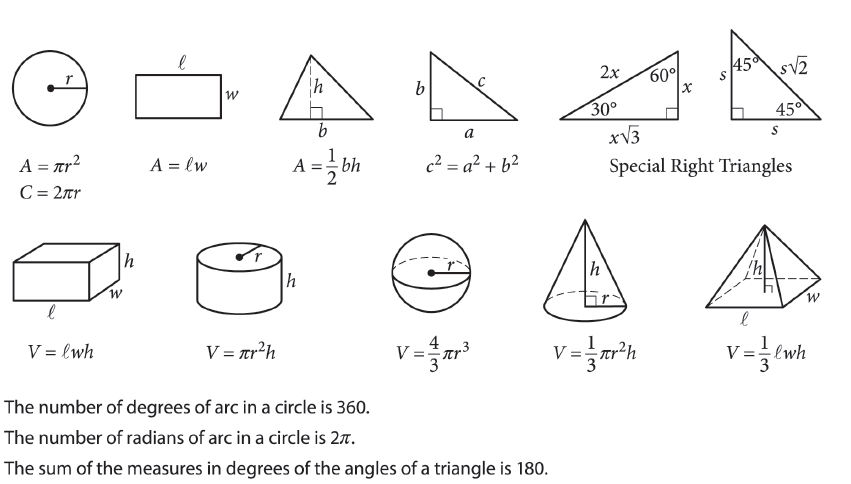
💡We’ve prepared a 7-Step Digital SAT Math Study Guide helping students to prepare their unique SAT Math Study Guide.
Free Digital SAT Prep Course
SFBS offers a Free Digital SAT Prep Online Course. The course goes through particular skills and knowledge testing points and improves your problem-solving skills and test-taking strategies.
SAT Geometry Topic 2: Lines, Angles and Triangles
Understanding the properties and relationships between lines, angles, and triangles is fundamental to mastering SAT Geometry questions. This lecture will cover essential concepts and formulas to help solve these types of problems efficiently.
Lines and Angles
Definitions:
- Point: An exact location in space.
- Line: A collection of points extending infinitely in both directions.
- Line Segment: A part of a line with two endpoints.
- Ray: A part of a line that starts at a point and extends infinitely in one direction.
Types of Angles:
- Acute Angle: Less than 90°.
- Right Angle: Exactly 90°.
- Obtuse Angle: Greater than 90° but less than 180°.
- Straight Angle: Exactly 180°.
- Reflex Angle: Greater than 180° but less than 360°.
Angle Relationships:
- Complementary Angles: Two angles whose measures add up to 90°.
- Supplementary Angles: Two angles whose measures add up to 180°.
- Vertical Angles: Opposite angles formed by two intersecting lines (always equal).
- Linear Pair: A pair of adjacent angles that form a straight line (supplementary).
Parallel and Perpendicular Lines
Definitions:
- Parallel Lines: Lines in a plane that never intersect and are always the same distance apart.
- Perpendicular Lines: Lines that intersect to form a right angle (90°).
Properties Involving Transversals:
- Corresponding Angles Postulate: If a transversal intersects two parallel lines, each pair of corresponding angles is equal.
- Alternate Interior Angles Theorem: If a transversal intersects two parallel lines, each pair of alternate interior angles is equal.
- Consecutive Interior Angles Theorem: If a transversal intersects two parallel lines, consecutive interior angles are supplementary.
- Alternate Exterior Angles Theorem: If a transversal intersects two parallel lines, each pair of alternate exterior angles is equal.
Triangles: Types and Properties
Classification by Sides:
- Equilateral Triangle: All sides and angles are equal (each angle is 60°).
- Isosceles Triangle: At least two sides are equal, and the angles opposite these sides are also equal.
- Scalene Triangle: All sides and angles are different.
Classification by Angles:
- Acute Triangle: All angles are less than 90°.
- Right Triangle: One angle is exactly 90°.
- Obtuse Triangle: One angle is greater than 90°.
Key Theorems:
- Triangle Sum Theorem: The sum of the angles in any triangle is 180°.
- Exterior Angle Theorem: The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles.
Special Properties of Triangles
Isosceles Triangle Theorem: The angles opposite the equal sides of an isosceles triangle are equal.
Pythagorean Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
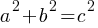
Special Right Triangles:
- 30-60-90 Triangle: The sides are in the ratio 1 : √3 : 2.
- 45-45-90 Triangle: The sides are in the ratio 1 : 1 : √2.
Congruence and Similarity in Triangles
Triangle Congruence Criteria:
- SSS (Side-Side-Side): Three sides of one triangle are equal to three sides of another triangle.
- SAS (Side-Angle-Side): Two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle.
- ASA (Angle-Side-Angle): Two angles and the included side of one triangle are equal to two angles and the included side of another triangle.
- AAS (Angle-Angle-Side): Two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle.
- HL (Hypotenuse-Leg for Right Triangles): The hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle.
Triangle Similarity Criteria:
- AA (Angle-Angle): Two angles of one triangle are equal to two angles of another triangle.
- SSS (Side-Side-Side): The corresponding sides of two triangles are proportional.
- SAS (Side-Angle-Side): Two sides are proportional, and the included angle is equal.
📚 San Francisco Business School offers a vast amount of FREE Digital SAT Prep Online materials. See it on the Free Digital SAT Prep Online Library.
Watch SAT Math Prep Online Course – Sample Lecture on YouTube
We have a sample 8-minute video lecture from our SAT Math Prep Online Course on YouTube. You can watch below.
Digital SAT Prep Online Course Program
San Francisco Business School offers a comprehensive Digital SAT Prep Online Course taught by 99th-percentile SAT Instructors and exam experts. The program cracks down each content domain, skills, and knowledge testing point through 1,000+ realistic Digital SAT Exam questions. You will see all the different types of questions that may appear in Digital SAT.
SAT Geometry Topic 3: Right Triangles and Trigonometry
Trigonometry deals with the relationships between the angles and sides of triangles, especially right triangles. Understanding these relationships is crucial for solving many SAT Geometry and Trigonometry problems, including those involving angles, heights, distances, and more.
Properties of Right Triangles
A right triangle is a triangle in which one angle is a right angle (90°). The side opposite the right angle is called the hypotenuse, and the other two sides are known as the legs.
Pythagorean Theorem:
For any right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides:
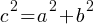
where c is the hypotenuse and a and b are the legs.
Special Right Triangles:
- 30-60-90 Triangle: The sides are in the ratio 1 : √3 : 2.
- 45-45-90 Triangle: The sides are in the ratio 1 : 1 : √2.
Basic Trigonometric Ratios
Trigonometric Ratios relate the angles of a right triangle to the lengths of its sides. The three basic trigonometric ratios are:
- Sine (sin):
sinθ=
- Cosine (cos):
cosθ=
- Tangent (tan):
tanθ=
These ratios are fundamental in solving right triangle SAT Geometry and Trigonometry problems.
Using Trigonometric Ratios to Solve Problems
To solve for missing sides or angles in right triangles:
- Finding Missing Sides: Use the trigonometric ratios to set up equations based on the given information.
Example:
If sinθ=0.5 and the hypotenuse is 10, then the opposite side is:
Opposite Side = sinθ × Hypotenuse = 0.5 × 10 = 0.5 × 10 = 5. - Finding Angles: Use the inverse trigonometric functions to determine the measure of an angle given two sides.
The Pythagorean Identity and Trigonometric Values
Pythagorean Identity:
If 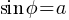 , and If
, and If 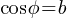
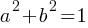
This identity is useful for finding one trigonometric value if another is known.
Key Trigonometric Values to Memorize for SAT Geometry and Trigonometry
sin, cos, tan for 0°, 30°, 45°, 60°, and 90°:
- sin0° = Error: WPMathPub plugin shortcode cannot be empty, sin30° =
 , sin45° =
, sin45° =  , sin60°=
, sin60°= , sin90° =
, sin90° = 
- cos0° =
 , cos30° =
, cos30° =  , cos45° =
, cos45° =  , cos60°=
, cos60°= , cos90° = Error: WPMathPub plugin shortcode cannot be empty
, cos90° = Error: WPMathPub plugin shortcode cannot be empty - tan0° = Error: WPMathPub plugin shortcode cannot be empty, tan30° =
 , tan45° =
, tan45° =  , tan60°=
, tan60°=  , tan90° = undefined
, tan90° = undefined
Applications of Right Triangle Trigonometry
- Word Problems: Trigonometry is often used in word problems involving heights, distances, and angles of elevation or depression.
- Coordinate Geometry: Trigonometry can be used to find slopes, distances, and angles between lines in coordinate planes.
Tips for SAT Geometry and Trigonometry Problems on Right Triangles and Trigonometry
- Remember the definitions of the trigonometric ratios and when to use them.
- Use the Pythagorean Theorem and trigonometric identities to simplify problems.
- Practice visualizing right triangles in different contexts, such as coordinate planes and word problems.
SAT Geometry & Trigonometry – Hack Points & Exercises – YouTube Video
You can view our SAT Geometry & Trigonometry YouTube video. We’ve gone through each of the 4 SAT Geometry & Trigonometry topics, provided the important points to know, and exercises for each as well.
Free Digital SAT Prep Course
SFBS offers a Free Digital SAT Prep Online Course. The course goes through particular skills and knowledge testing points and improves your problem-solving skills and test-taking strategies.
SAT Geometry Topic 4: Circles
A circle is a set of all points in a plane that are equidistant from a fixed point called the center. Understanding the properties and formulas related to circles is essential for solving many SAT Geometry problems on the SAT.
Properties of Circles
- Radius (r): The distance from the center of the circle to any point on the circle.
- Diameter (d): The distance across the circle through its center; d = 2r
- Circumference (C): The distance around the circle; C = 2πr.
- Chord: A line segment with both endpoints on the circle.
- Arc: A portion of the circumference of a circle.
- Sector: A region enclosed by two radii of a circle and their intercepted arc.
- Segment: A region enclosed by a chord and the arc it subtends.
- Central Angle: An angle whose vertex is at the center of the circle.
- Inscribed Angle: An angle whose vertex is on the circle and whose sides are chords.
Formulas Related to Circles
Circumference and Area:
- Circumference:
C=2πr
or
C=πd - Area:
A=
Length of an Arc:
Formula:
Arc Length = 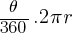
where θ is the central angle in degrees.
Area of a Sector:
Formula:
Area of a Sector = 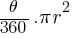
Equation of a Circle in the Coordinate Plane:
Standard Form:
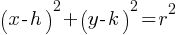 where (h,k) is the center of the circle and r is the radius.
where (h,k) is the center of the circle and r is the radius.
🖋️ Standard form of a circle is a frequently occurring SAT Geometry concept in SAT.
Angles and Arcs in Circles
Central Angles and Arc Measures:
- A central angle is equal to the measure of its intercepted arc.
Inscribed Angles:
- An inscribed angle is half the measure of its intercepted arc.
- Angles inscribed in a semicircle are right angles (90°).
Angles Formed by Chords, Secants, and Tangents:
- The angle formed by two intersecting chords is half the sum of the measures of the arcs intercepted by the angle and its vertical angle.
- The angle formed by a tangent and a chord through the point of contact is half the measure of the intercepted arc.
Tangents and Their Properties
Definition of a Tangent:
A tangent to a circle is a line that touches the circle at exactly one point.
Properties of Tangents:
A tangent is perpendicular to the radius drawn to the point of tangency.
Two tangents drawn to a circle from an external point are equal in length.
Tangent-Secant and Tangent-Tangent Angle Theorems:
The angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
Solving SAT Geometry Problems Involving Circles
Common Problem Types:
Finding circumference, area, or arc length.
Solving for angles formed by tangents, chords, or secants.
Applying the properties of inscribed angles and central angles.
Word problems involving real-world applications of circles.
Strategies for SAT Geometry and Trigonometry Problems
We recommend the following tips and strategies for solving SAT Geometry and Trigonometry problems:
- Draw diagrams to visualize the problem.
- Use the appropriate formulas based on the given information.
- Check for relationships between angles, arcs, and chords.
Tips for SAT Geometry Problems on Circles
- Familiarize yourself with all circle formulas and properties.
- Pay attention to the specific details given in the problem (e.g., diameter vs. radius).
- Practice recognizing and applying the properties of tangents, chords, and arcs.
Digital SAT Prep Online Course Program
San Francisco Business School offers a comprehensive Digital SAT Prep Online Course taught by 99th-percentile SAT Instructors and exam experts. The program cracks down each content domain, skills, and knowledge testing point through 1,000+ realistic Digital SAT Exam questions. You will see all the different types of questions that may appear in Digital SAT.
SAT Geometry and Trigonometry Exercises
There are four SAT Geometry and Trigonometry Exercises below, one for each skill and knowledge testing below. To improve your math skills, we do not recommend using a calculator when solving these SAT Geometry and Trigonometry Exercises.
Exercise I. One side of a rectangle and a square are common. The area of the rectangle is two times the area of the square. If the perimeter of the rectangle is 10 units greater than the perimeter of the square, what is the length of the rectangle in units?
Exercise II.
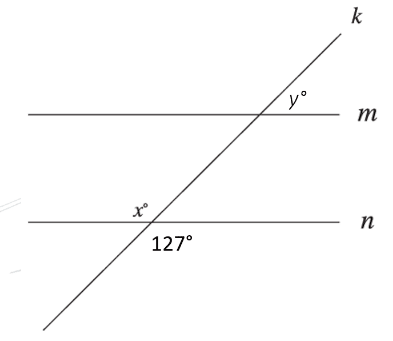
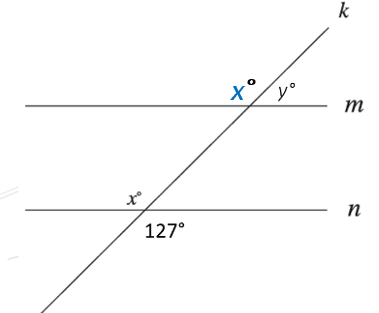
In the figure, line m is parallel to line n, and line k intersects both lines. What is the value of x + y ?
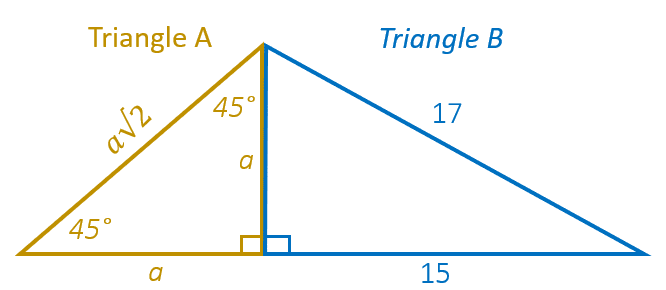
Exercise III. One leg of an isosceles right triangle A is common with the shortest leg of another right triangle B. The length of the longest side of the triangle B is 17, and longer leg length is 15. What is the length of the longest side of triangle A?
Exercise IV. The graph of 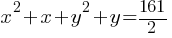 in the xy-plane is a circle. What is the area of the circle?
in the xy-plane is a circle. What is the area of the circle?
💡You can see our Free SAT Math Exercises which has 50 exercises on all SAT Math domains.
Note: You can use a calculator in this SAT Math Exercise
💡Do not forget to visit SAT Math Exercises which has 50 exercises on all SAT Math domains. It’s for free!
SAT Geometry and Trigonometry Practice Test
We’ve listed 4 hard SAT Geometry and Trigonometry practice test questions below. Note that this test does not resemble the typical question difficulty distribution on an SAT Geometry and Trigonometry domain. Instead, we wanted to show you the hardest SAT Math Geometry and Trigonometry questions you may see on the SAT.
Besides, since these are the hardest questions for the SAT Geometry and Trigonometry, it is very normal that you will spend longer than usual time to solve each question. It is also super normal that you may score lower than your previous SAT Geometry and Trigonometry Practice tests in this one. Because a typical Digital SAT Math Practice Test covers easy, medium, and hard questions. However, this one contains only the hardest questions.
Question 1
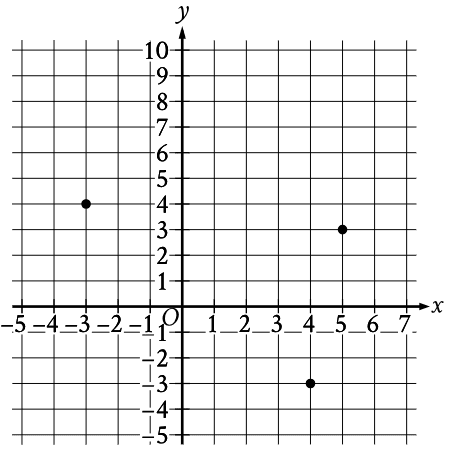
What is the area, in square units, of the triangle formed by connecting the three points shown?
Skill and Knowledge Testing Point: Area and volume
SAT Geometry and Trigonometry Practice – Question 2
In triangle RST, angle T is a right angle, point L lies on 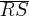 , point K lies on
, point K lies on 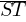 , and
, and 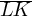 is parallel to
is parallel to 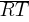 . If the length of
. If the length of 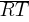 is 72 units, the length of
is 72 units, the length of 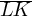 is 24 units, and the area of triangle RST is 792 square units, what is the length of
is 24 units, and the area of triangle RST is 792 square units, what is the length of 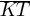 , in units?
, in units?
Skill and Knowledge Testing Point: Lines, angles, and triangles
Question 3
Triangle ABC is similar to triangle DEF, where A corresponds to D and C corresponds to F. Angles C and F are right angles. If 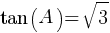 and DF = 125, what is the length of
and DF = 125, what is the length of 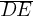 ?
?
A. 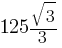
B. 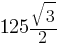
C. 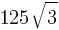
D. 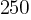
Skill and Knowledge Testing Point: Right triangles and trigonometry
Question 4
A circle in the xy-plane, the graph of 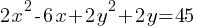 is a circle. What is the radius of the circle?
is a circle. What is the radius of the circle?
A. 5
B. 6.5
C. 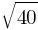
D. 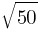
Skill and Knowledge Testing Point: Circles
SAT Geometry and Trigonometry Practice Test Answers and Rationales
We’ve created a comprehensive answers and rationales PDF file for these SAT Geometry and Practice questions. If you can fill in your name and email below, we can send it to your email in minutes. Note that, the PDF you will receive will have 19 questions from all SAT Math domains. The last 4 questions (Questions 16-19) are answers and rationales for this SAT Geometry and Trigonometry Practice Test.
Note that, the email may hit your junk or spam folders, please check your junk and spam folders and if you did not receive it, please email us at support@sanfranciscobs.com.
💡Do not forget to visit SAT Math Practice Test – Hardest Questions. Assess your SAT Math skills with the hardest questions you may see on SAT Math.
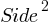
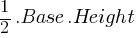
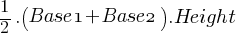
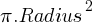
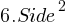
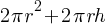 (top and bottom circles + lateral area)
(top and bottom circles + lateral area)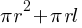 (base area + lateral area, where l is the slant height)
(base area + lateral area, where l is the slant height)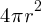



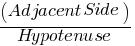

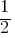 , sin45° =
, sin45° = 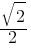 , sin60°=
, sin60°=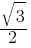 , sin90° =
, sin90° = 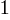
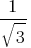 , tan45° =
, tan45° = 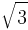 , tan90° = undefined
, tan90° = undefined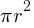
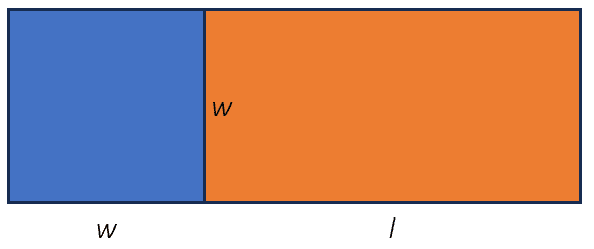
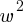
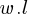
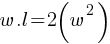 . If we divide both sides by w;
. If we divide both sides by w;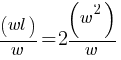 . This yields;
. This yields;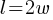 . We found the relationship between the length and width of the rectangle.
. We found the relationship between the length and width of the rectangle.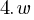
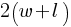
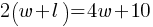 . We can substitute
. We can substitute 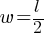 and this yields;
and this yields;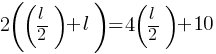 . This yields;
. This yields;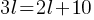 . If we subtract 2l from both sides;
. If we subtract 2l from both sides;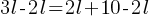 . This yields;
. This yields;
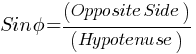 . For an isosceles right triangle, the angles will be 45°-45°-90°.
. For an isosceles right triangle, the angles will be 45°-45°-90°.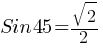 . Therefore;
. Therefore;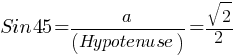 . If we do cross-multiplication;
. If we do cross-multiplication; . If we divide both sides by
. If we divide both sides by  ;
;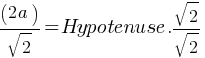 . This yields;
. This yields;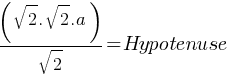 . This yields;
. This yields;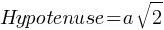
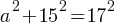 . If we isolate the
. If we isolate the 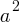 ;
;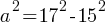 . This yields;
. This yields;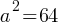 . If we apply square root on both sides;
. If we apply square root on both sides;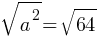 . This yields;
. This yields;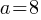 .
.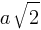 . If we substitute the value of a;
. If we substitute the value of a;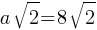
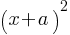 as
as 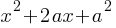 . Therefore, we can rewrite;
. Therefore, we can rewrite;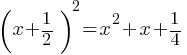 . If we subtract
. If we subtract 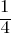 from both sides;
from both sides;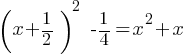 .
.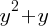 part as follows;
part as follows;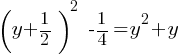 .
.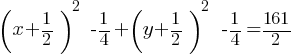 . This yields;
. This yields;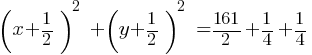 . This yields;
. This yields;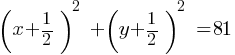 . This is now in the standard form of a circle
. This is now in the standard form of a circle 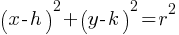 , where
, where 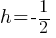 ,
, 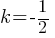 and
and 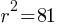 .
.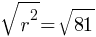 . This yields;
. This yields;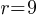 .
.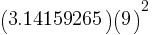 . This yields;
. This yields;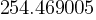 . (You can round this to 254.47.)
. (You can round this to 254.47.)