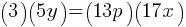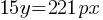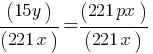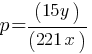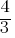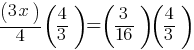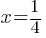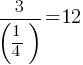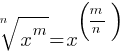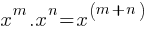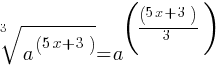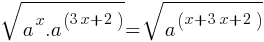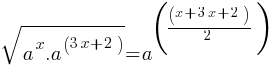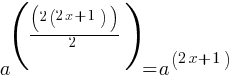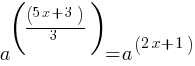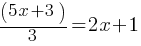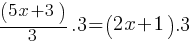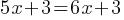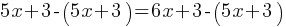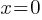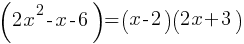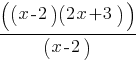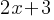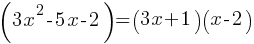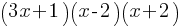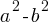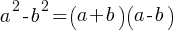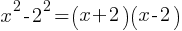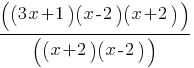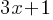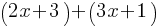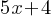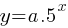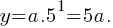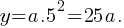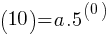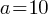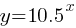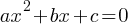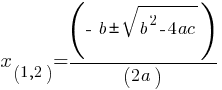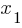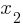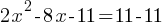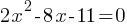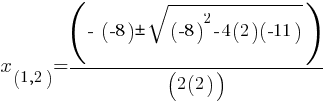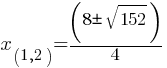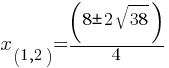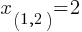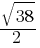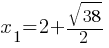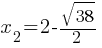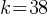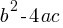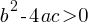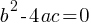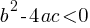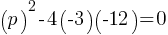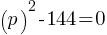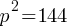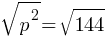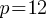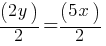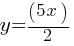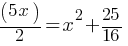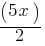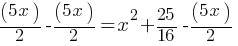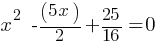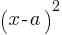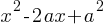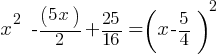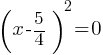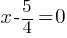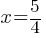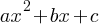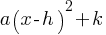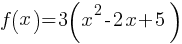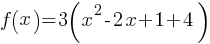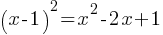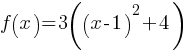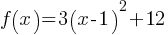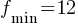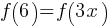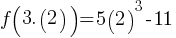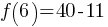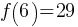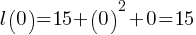SAT Advanced Math – Important Points and SAT Advanced Math Practice Test
There are 44 SAT Math questions in the SAT Exam. 13 to 15 of these 44 questions come from the SAT Advanced Math content domain. Approximately 30-35% of the SAT Math questions come from the SAT Advanced Math. Advanced Math is a little bit harder than SAT Algebra. However, having a solid background and solving as many SAT Advanced Math practices as possible will improve your SAT Advanced Math scores.
In this article
📌 Hint: Do not skip this article, you will find FREE Digital SAT Math Prep resources throughout the article.
We’ve listed the most important and frequently occurring concepts in this SAT Advanced Math post. You will see SAT Advanced Math practice test questions and exercises, totaling 27 SAT Advanced Math questions with rationales for FREE.
💡You might be interested in reading the Digital SAT Math Prep post.
SAT Advanced Math Content Domain
Advanced Math focuses on the math you’ll need to pursue further study in disciplines such as science or economics and for career opportunities in the STEM fields of science, technology, engineering, and math. SAT Advanced Math area measures skills and knowledge central for progression to more advanced math courses, including demonstrating an understanding of absolute value, quadratic, exponential, polynomial, rational, radical, and other nonlinear equations.
💡You might be interested in reading the Digital SAT Math Ultimate Guide post. We have provided further details about the SAT Math structure, examples of easy, medium, and hard questions, answers, rationales, and frequently asked questions about the SAT Math.
Anna B. Scored 800 on SAT Math!
Anna B. is one of our thousands of successful SAT students. She scored 800 on SAT Math. You can watch her SAT story.

SAT Advanced Math Skills and Knowledge Testing Points
The SAT exam will have around 13 to 15 questions from the Advanced Math content domain. There are 3 skills and knowledge testing points in the SAT Advanced Math content domain:
- Equivalent expressions
- Nonlinear equations in one variable and systems of equations in two variables
- Nonlinear functions
Let’s review each skill and knowledge point and see some SAT Advanced Math Exercises for each.
🗎 Download the 15-page Digital SAT Math Formula Sheet.
1. Equivalent Expressions
Equivalent expressions are algebraic expressions that, despite having different forms, produce the same result for any value of the variable(s).
Importance: Understanding equivalent expressions is crucial for simplifying algebraic SAT Advanced Math problems, solving equations, and performing algebraic manipulations.
Basic Principles of Equivalent Expressions
Commutative Property:
Addition: a+b = b+a
Multiplication: a×b = b×a
Associative Property:
Addition: (a+b)+c=a+(b+c)
Multiplication: (a×b)×c=a×(b×c)
Distributive Property:
a(b+c) = ab + ac
Recognizing Equivalent Expressions
Simplification: Combine like terms and use properties to simplify expressions.
Example 1: Simplify 2x + 3x −4 + x.
Solution: Combine like terms: 2x+3x+x−4=6x−4.
Equivalent Expression: 6x−4
Techniques for Finding Equivalent Expressions
Factoring and Expanding: Use the distributive property to factor and expand expressions.
Example 2: Find an equivalent expression for 3(x+2)+4x.
Solution: Expand 3(x+2)=3x+6, then add 4x:
3x+6+4x = 7x+6
Equivalent Expression: 7x+6
Equivalent Expressions Practice Problems
Example 3: Identify if the expressions 4(x+1)−2 and 4x+2 are equivalent.
Solution: Expand 4(x+1)−2=4x+4−2 = 4x+2
Equivalent: Yes, both expressions simplify to 4x+2.
Example 4: Determine the equivalent expression for 2(a+b)−3(b−a).
Solution:
Expand: 2a+2b−3b+3a = 5a−b
Equivalent Expression: 5a−b.
Application in SAT Advanced Math Problems
Strategy: Recognize and use equivalent expressions to simplify complex problems and solve equations efficiently.
Example 5: Solve for x if 3x+4=2x+8.
Solution: Rearrange to form an equivalent expression: 3x−2x = 8−4.
Solve: x = 4.
Common Mistakes to Avoid
Ignoring Parentheses: Remember to apply the distributive property correctly when parentheses are involved.
Forgetting to Combine Like Terms: Always combine like terms to simplify the expression fully.
Summary and Key Takeaways
- Equivalent expressions represent the same quantity and are essential for algebraic manipulation.
- Mastery of properties (commutative, associative, distributive) is crucial in recognizing and forming equivalent expressions.
- Practice identifying and creating equivalent expressions to build confidence for the SAT Advanced Math section.
💡We’ve prepared a 7-Step Digital SAT Math Study Guide helping students to prepare their unique SAT Math Study Guide.
SAT Advanced Math Exercises for Equivalent Expressions
To improve your math skills, we do not recommend using a calculator when solving these SAT Advanced Math Exercises.
Exercise I. 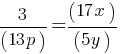
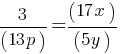
The given equation relates the positive numbers p, x, and y. Write the p-value in terms of x and y.
Exercise II. 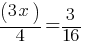
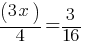
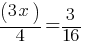
What is the value of 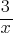
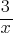
Exercise III. 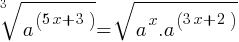
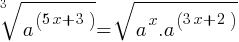
What is the value of x?
Exercise IV. 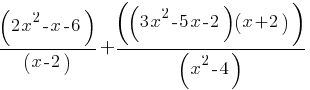
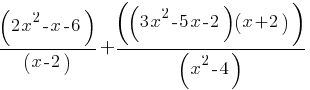
Simplify the given expression.
💡You can see our Free SAT Math Exercises which has 50 exercises on all SAT Math domains.
📚 San Francisco Business School offers a vast amount of FREE Digital SAT Prep Online materials. See it on the Free Digital SAT Prep Online Library.
Free Digital SAT Prep Course
SFBS offers a Free Digital SAT Prep Online Course. The course goes through particular skills and knowledge testing points and improves your problem-solving skills and test-taking strategies.
2. Nonlinear Equations in One Variable and Systems of Equations in Two Variables
Nonlinear Equations in One Variable
A nonlinear equation in one variable is an equation in which the variable is raised to a power other than one, appears in the denominator, or is part of a function like a square root or absolute value. Common examples include quadratic equations, cubic equations, and equations involving square roots or absolute values.
We’ve listed types of nonlinear equations and how to solve these SAT Advanced Math questions below.
Types of Nonlinear Equations
Quadratic Equations: 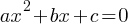
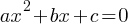
Cubic Equations: 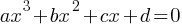
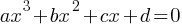
Equations Involving Square Roots: 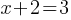
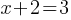
Equations with Absolute Values: |x-3| = 5
Solving Nonlinear Equations
Quadratic Equations:
Factoring: Find two numbers that multiply to ac (coefficient of x2 times constant term) and add to b (coefficient of x).
Quadratic Formula: 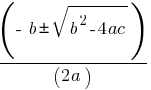
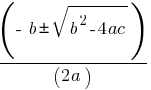
Completing the Square: Rewriting the equation in the form 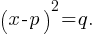
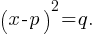
💡Tip: Quadratic Equations and Formula is a frequently occurring SAT Advanced Math concept in SAT exam.
Example 1: Solve 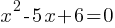
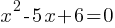
Solution: 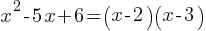
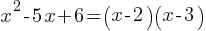
Therefore, x = 2 or x = 3.
Equations with Square Roots:
Isolate the square root on one side of the equation and then square both sides.
Example 2: Solve 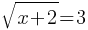
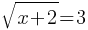
Solution: Square both sides: x + 2 = 9
x = 7
Equations with Absolute Values:
Split into two cases, one where the expression inside the absolute value is positive and one where it is negative.
Example 3: Solve ∣x−3∣ = 5.
Solution: x – 3 = 5 or x – 3 = – 5
x = 8 or x = -2
Systems of Equations in Two Variables
A system of equations consists of two or more equations with the same set of variables. Solving systems of equations means finding the set of values for the variables that satisfy all equations in the system.
Types of Systems
Linear-Linear Systems: Both equations are linear.
Linear-Nonlinear Systems: One equation is linear, and the other is nonlinear (like a quadratic).
Solving Systems of Equations in SAT Advanced Math
Substitution Method:
Solve one equation for one variable and substitute that expression into the other equation.
Example 4: Solve the system:
y=2x+3
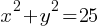
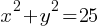
Solution: Substitute y = 2x + 3 into the second equation:
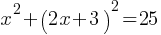
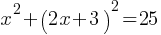
Expand and simplify:
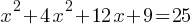
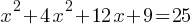
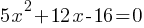
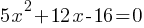
Solve the quadratic equation using the quadratic formula or factoring.
Elimination Method:
Add or subtract the equations to eliminate one of the variables.
Example 5: Solve the system:
x+y=7
x−y=1
Solution: Add the two equations to eliminate y:
2x = 8 ⇒ x = 4
Substitute x=4 back into x+y=7
4 + y = 7 ⇒ y = 3
The solution is x = 4, y = 3
💡You can see our Free SAT Math Exercises which has 50 exercises on all SAT Math domains.
Watch SAT Math Prep Online Course – Sample Lecture on YouTube
We have a sample 8-minute video lecture from our SAT Math Prep Online Course on YouTube. You can watch below.

SAT Advanced Math Exercises for Nonlinear Equations in One Variable and Systems of Equations in Two Variables
To improve your math skills, we do not recommend using a calculator when solving these SAT Advanced Math Exercises.
Exercise I. Two variables, x, and y are related such that for each increase of 1 in the value of x, the value of y increases by a factor of 5. When x=0, y=10. Write the y in terms of x.
Exercise II. 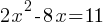
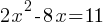
One solution to the given equation can be written as 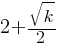
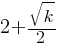
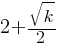
Exercise III. 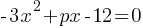
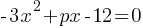
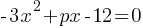
In the given equation, p is a constant. The equation has exactly one solution. What is the value of p?
Exercise IV. 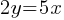
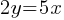
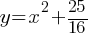
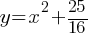
A solution to the given system of equations is (x, y), where x>0. What is the value of x?
Digital SAT Prep Online Course Program
San Francisco Business School offers a comprehensive Digital SAT Prep Online Course taught by 99th-percentile SAT Instructors and exam experts. The program cracks down each content domain, skills, and knowledge testing point through 1,000+ realistic Digital SAT Exam questions. You will see all the different types of questions that may appear in Digital SAT.
3. Nonlinear Functions
Nonlinear functions are those whose graphs are not straight lines. These functions have at least one variable raised to a power other than one, multiplied by itself, or in some other configuration that creates a curve rather than a line. In SAT Advanced Math, understanding nonlinear functions involves recognizing their different forms and how they behave on a graph.
Key Characteristics of Nonlinear Functions:
- Nonlinear Graphs: The graphs of nonlinear functions can be parabolas, circles, ellipses, hyperbolas, or any other shape that is not a straight line.
- Variable Powers: At least one variable is raised to a power other than one (e.g., x², x³).
- Multiple Solutions: Nonlinear functions can have multiple x-intercepts, y-intercepts, or roots.
- Changes in Direction: Nonlinear graphs can change direction, unlike linear graphs that are consistently increasing or decreasing.
Common Types of Nonlinear Functions in SAT Advanced Math
1. Quadratic Functions
Form: f(x) = ax² + bx + c
Graph: Parabola (U-shaped curve)
Vertex: The highest or lowest point of the parabola.
Examples:
f(x) = x² – 4x + 3
Graph this function: The parabola opens upwards because the coefficient of x² is positive. The roots are where the function crosses the x-axis.
2. Cubic Functions
Form: f(x) = ax³ + bx² + cx + d
Graph: S-shaped curve with one or more turns.
Examples:
f(x) = x³ − 3x² + 2x
Graph this function: The curve starts from the lower left, turns upward, turns again, and moves downward or upward depending on the coefficients.
3. Exponential Functions
Form: f(x) = 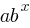
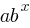
Graph: Exponential growth or decay curve.
Examples:
f(x)=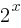
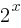
f(x)=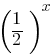
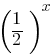
These functions rapidly increase or decrease and never touch the x-axis.
4. Absolute Value Functions
Form: f(x) = ∣ax+b∣
Graph: V-shaped graph.
Examples:
f(x) = ∣x−2∣
Graph this function: The graph has a vertex at x=2 and opens upwards.
5. Rational Functions
Form: f(x) = 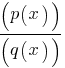
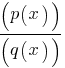
Graph: Can have asymptotes and undefined points.
Examples:
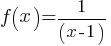
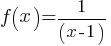
Graph this function: The function has a vertical asymptote at x=1 and a horizontal asymptote at y=0.
Examples and Practice Problems
Example 1: Quadratic Function
Problem: Graph the function 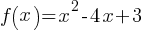
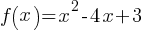
Solution:
Identify the coefficients: a=1, b=−4, c=3.
Find the roots using the quadratic formula: x=1 and x=3.
The vertex is at (2,−1).
The parabola opens upwards.
Example 2: Exponential Function
Problem: Solve for x in the equation 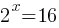
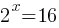
Solution: Rewrite 16 as 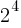
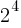
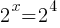
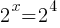
Example 3: Rational Function
Problem: Determine the domain of the function 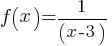
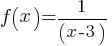
Solution: The function is undefined when the denominator is zero, so x ≠ 3. The domain is all real numbers except x = 3.
Graphing Nonlinear Functions
Graphing nonlinear functions involves plotting points and understanding the shape of the function. Here are the steps to graph a nonlinear function:
- Identify the function type (quadratic, cubic, etc.)
- Determine key features: roots, intercepts, asymptotes, vertex, etc.
- Plot critical points and sketch the graph based on these points.
SAT Advanced Math Hack Points & Exercises YouTube Video
You can view our SAT Advanced Math YouTube video. We’ve gone through each of the 5 SAT Advanced Math topics, provided the important points to know, and exercises for each as well.
SAT Advanced Math Exercises for Nonlinear Functions
To improve your math skills, we do not recommend using a calculator when solving these SAT Advanced Math Exercises.
Exercise I. 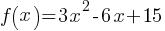
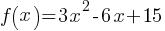
The given equation defines the function f. What is the minimum value of f(x)?
Exercise II. The function f is defined by 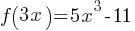
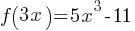
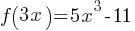
Exercise III. The function 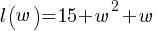
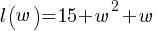
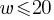
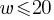
Free Digital SAT Prep Course
SFBS offers a Free Digital SAT Prep Online Course. The course goes through particular skills and knowledge testing points and improves your problem-solving skills and test-taking strategies.
SAT Advanced Math Practice Test
We’ve listed 3 hard SAT Advanced Math practice test questions below. Note that this test does not resemble the typical question difficulty distribution on an SAT Advanced Math domain. Instead, we wanted to show you the hardest SAT Advanced Math questions you may see on the SAT.
Besides, since these are the hardest questions for the SAT Advanced Math, it is very normal that you will spend longer than usual time to solve each question. It is also super normal that you may score lower than your previous SAT Advanced Math Practice tests in this one. Because a typical Digital SAT Math Practice Test covers easy, medium, and hard questions. However, this one contains only the hardest questions.
Question 1
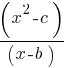
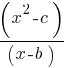
In the expression above, b and c are positive integers. If the expression is equivalent to x+b and x ≠ b, which of the following could be the value of c ?
A. 4
B. 6
C. 8
D. 10
Skill and Knowledge Testing Point: Equivalent expressions
Question 2
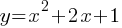
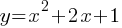
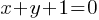
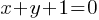
If 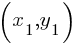
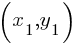
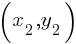
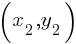
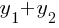
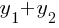
A. -3
B. -2
C. -1
D. 1
Skill and Knowledge Testing Point: Nonlinear equations in one variable and systems of equations in two variables
Question 3
| x | 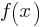 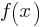 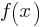 |
| 1 | 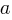 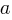 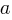 |
| 2 | 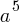 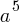 |
| 3 | 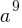 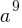 |
For the exponential function 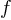
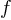
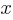
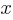
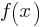
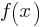
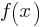
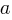
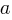
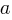
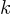
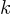
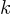
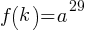
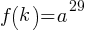
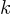
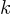
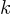
Skill and Knowledge Testing Point: Nonlinear functions
SAT Advanced Math Practice Test Answers and Rationales
We’ve created a comprehensive answers and rationales PDF file for these SAT Advanced Math questions. If you can fill in your name and email below, we can send it to your email in minutes. Note that, the PDF you will receive will have 19 questions from all SAT Math domains. Questions 6, 7, and 8 (Questions 6-8) are answers and rationales for this SAT Advanced Math Practice Test.
Note that, the email may hit your junk or spam folders, please check your junk and spam folders and if you did not receive it, please email us at support@sanfranciscobs.com.
💡Do not forget to visit SAT Math Practice Test – Hardest Questions. Assess your SAT Math skills with the hardest questions you may see on SAT Math.