SAT Algebra – Important Points and SAT Algebra Practice Test
There are 44 SAT Math questions in the SAT Exam. 13 to 15 of these 44 questions come from the SAT Algebra content domain. This makes the Algebra content domain 30-35% of the SAT Math. Therefore, having a solid SAT Algebra background and solving as many SAT Algebra Practice Tests as possible is crucial to having a high SAT Math score.
In this article
📌 Hint: Do not skip this article, you will find FREE Digital SAT Math Prep resources throughout the article.
We’ve listed the most important and frequently occurring concepts in this SAT Algebra post. You will see SAT Algebra practice test questions and exercises, in total 31 SAT Algebra questions with rationales all for FREE.
💡You might be interested in reading the Digital SAT Math Prep post.
SAT Algebra Content Domain
Algebra is a branch of mathematics in which arithmetical operations and formal manipulations are applied to abstract symbols rather than specific numbers. Algebra is the first content domain in the SAT Math. In the SAT Algebra domain, the College Board assesses the abilities of students in solving and creating linear equations and inequalities as well as analyzing and fluently solving equations and systems of equations using multiple techniques.
💡You might be interested in reading the Digital SAT Math Ultimate Guide post. We have provided further details about the SAT Math structure, examples of easy, medium, and hard questions, answers, rationales, and frequently asked questions about the SAT Math.
👉 Take our full-length FREE SAT Practice Test, see where you stand!
Anna B. Scored 800 on SAT Math!
Anna B. is one of our thousands of successful SAT students. She scored 800 on SAT Math. You can watch her SAT story.
SAT Algebra Skills and Knowledge Testing Points
The SAT exam will have around 13 to 15 questions from the Algebra content domain. There are 5 skills and knowledge testing points in the Algebra content domain:
- Linear equations in one variable
- Linear equations in two variables
- Linear functions
- Systems of two linear equations in two variables
- Linear inequalities in one or two variables
Let’s review each skill and knowledge point and see some SAT Algebra Exercises for each.
🗎 Download the 15-page Digital SAT Math Formula Sheet.
1. Linear Equations in One Variable – Important Points
A linear equation in one variable is an equation that can be expressed in the form:
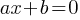
Where:
 and
and  are constants and
are constants and  ≠ Error: WPMathPub plugin shortcode cannot be empty.
≠ Error: WPMathPub plugin shortcode cannot be empty. is the variable.
is the variable.
The general solution to a linear equation in one variable will yield a single value for 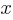 .
.
How to Solve SAT Algebra Linear Equations
There are three simple steps to solve linear equations:
- Isolate the variable: Use addition, subtraction, multiplication, and division to get the variable by itself on one side of the equation.
- Simplify: Combine like terms and simplify both sides if necessary.
- Check your solution: Substitute the found value into the original equation to verify correctness.
💡We’ve prepared a 7-Step Digital SAT Math Study Guide helping students to prepare their unique SAT Math Study Guide.
SAT Math Algebra Exercises for Linear Equations in One Variable
To improve your math skills, we do not recommend using a calculator when solving these SAT Math Algebra Exercises.
Exercise I. 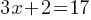
Exercise II. 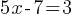
Exercise III. 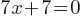
Exercise IV. 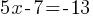
Exercise V. 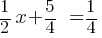
Exercise VI. Ethan has $15. He gets 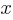 dollars from his grandfather. If Ethan has $35 now, what is the value of
dollars from his grandfather. If Ethan has $35 now, what is the value of 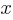 ?
?
💡You can see our Free SAT Math Exercises which has 50 exercises on all SAT Math domains.
2. Linear Equations in Two Variables – Important Points
A linear equation in two variables can be expressed in the form:
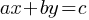
Where:
 ,
, and
and  are constants.
are constants. and
and  are variables.
are variables.
Graphing SAT Algebra Linear Equations
- The graph of a linear equation in two variables is a straight line.
- The coefficients
 and
and  determine the slope of the line, while
determine the slope of the line, while  affects its position on the graph.
affects its position on the graph.
Slope-Intercept Form:
- A common way to express a linear equation is the slope-intercept form:
 where
where  is the slope and
is the slope and  is the y-intercept (the point where the line crosses the y-axis).
is the y-intercept (the point where the line crosses the y-axis).
🖋️ Slope-intercept form is a frequently occurring concept in SAT Math.
- Parallel Lines: Slopes of parallel lines are the same.
- Perpendicular Lines: The product of the perpendicular lines is (-1).
Free Digital SAT Prep Course
SFBS offers a Free Digital SAT Prep Online Course. The course goes through particular skills and knowledge testing points and improves your problem-solving skills and test-taking strategies.
SAT Algebra Exercises for Linear Equations in Two Variables
To improve your math skills, we do not recommend using a calculator when solving these SAT Math Exercises.
Exercise I. 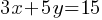 . What is the y-intercept of this graph?
. What is the y-intercept of this graph?
Exercise II. 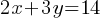 . What is the x-intercept of this graph?
. What is the x-intercept of this graph?
Exercise III. 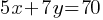 .
. 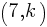 and
and 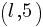 are two possible solutions to the equation. What is the value of
are two possible solutions to the equation. What is the value of 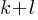 ?
?
Exercise IV. 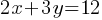 . Grapf of line m is given. A line k is parallel to line m. What is the slope of line k?
. Grapf of line m is given. A line k is parallel to line m. What is the slope of line k?
Exercise V. 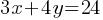 . If the line h is perpendicular to the given equation’s graph, what is the slope of line h?
. If the line h is perpendicular to the given equation’s graph, what is the slope of line h?
Exercise VI. A line passes through (0, 4) and the slope of the line is 2. What is the equation of this line?
SAT Algebra Hack Points & Exercises YouTube Video
You can view our SAT Algebra YouTube video. We’ve gone through each of the 5 SAT Algebra topics, provided the important points to know, and exercises for each as well.
💡You might be interested in seeing our Digital SAT Math Practice Test. It covers the hardest questions you may see on the SAT Math exam for each skill and knowledge testing point!
3. Linear Functions – Important Points
A linear function is a function that creates a straight line when graphed on the xy-plane.
- The general form of a linear function is:
 where
where  is the slope and
is the slope and  is the y-intercept ((0, b), the value of f(x) when x = 0).
is the y-intercept ((0, b), the value of f(x) when x = 0). - The slope (m) of a linear function indicates the steepness of the line. It can be calculated as:

The slope can be positive, negative, zero, or undefined:
-
- Positive slope: The line rises as it moves from left to right.
- Negative slope: The line falls as it moves from left to right.
- Zero slope: The line is horizontal.
- Undefined slope: The line is vertical.
SFBS Digital SAT Prep Online Course Program
San Francisco Business School offers a comprehensive Digital SAT Prep Online Course taught by 99th-percentile SAT Instructors and exam experts. The program cracks down each content domain, skills, and knowledge testing point through 1,000+ realistic Digital SAT Exam questions. You will see all the different types of questions that may appear in Digital SAT.
SAT Algebra Exercises for Linear Functions
To improve your math skills, we do not recommend using a calculator when solving these SAT Algebra Exercises.
Exercise I. The graph of y = f(x) passes through the points (1, 4) and (3, 10). What is the function f ?
Exercise II. The function f is defined by the equation 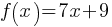 . What is the value of f(x) when
. What is the value of f(x) when 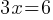 ?
?
Exercise III. An electrician charges a $40 fixed fee plus $25 per hour. If the function h models the total fee for the electrician for t hours of work, write the function h.
Exercise IV. The function f is defined by 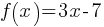 . What is the y-intercept of the graph of
. What is the y-intercept of the graph of 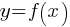 in the xy-plane?
in the xy-plane?
Exercise V. The graph of y = f(x) and y=h(x) are perpendicular to each other in the xy-plane. Function f is defined by 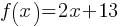 . If
. If 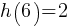 , write the y=h(x) function.
, write the y=h(x) function.
Exercise VI. The function 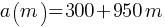 models the altitude of an airplane m minutes after takeoff. According to the model, what is the altitude of the airport where the airplane took off?
models the altitude of an airplane m minutes after takeoff. According to the model, what is the altitude of the airport where the airplane took off?
📚 San Francisco Business School offers a vast amount of FREE Digital SAT Prep Online materials. See it on the Free Digital SAT Prep Online Library.
4. Systems of Two Linear Equations in Two Variables – Important Points
A system of two linear equations in two variables consists of two equations that can be represented in the form:
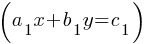
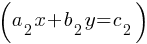
where x and y are variables, and 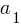 ,
, 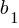 ,
, 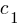 ,
, 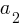 ,
, 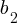 , and
, and 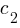 are constants.
are constants.
Graphical Interpretation: Each equation represents a straight line in the coordinate plane. The solution to the system is the point where the two lines intersect.
How to Solve SAT Algebra Systems of Equations
There are three main methods to solve a system of linear equations:
- Graphing:
- Rewrite both equations in slope-intercept form (y = mx + b).
- Graph each line on the same coordinate plane.
- Identify the intersection point, which is the solution.
- Substitution
- Solve one equation for one variable.
- Substitute that expression into the other equation.
- Solve for the remaining variable.
- Substitute back to find the other variable.
- Elimination
- Align the equations.
- Multiply one or both equations to make the coefficients of one variable opposite.
- Add or subtract the equations to eliminate one variable.
- Solve for the remaining variable.
- Substitute back to find the other variable.
Watch SAT Math Prep Online Course – Sample Lecture on YouTube
We have a sample 8-minute video lecture from our SAT Math Prep Online Course on YouTube. You can watch below.
Free Digital SAT Prep Course
SFBS offers a Free Digital SAT Prep Online Course. The course goes through particular skills and knowledge testing points and improves your problem-solving skills and test-taking strategies.
SAT Algebra Exercises for Systems of Two Linear Equations in Two Variables
To improve your math skills, we do not recommend using a calculator when solving these SAT Algebra Exercises.
Exercise I. 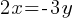
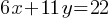
The solution to the given system of equations is (x, y). What is the value of y)
Exercise II. 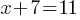
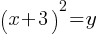
For the given system of equations, what is the value of y ?
Exercise III. 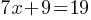
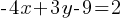
The solution to the given system of equations is (x, y). What is the value of x + y?
Exercise IV. 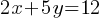
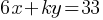
In the given system of equations, k is a constant. If the system has no solution, what is the value of k?
💡You might be interested in seeing our Digital SAT Math Practice Test. It covers the hardest questions you may see on the SAT Math exam for each skill and knowledge testing point!
5. Linear Inequalities in One or Two Variables – Important Points
A linear inequality is similar to a linear equation but uses inequality signs (>, <, ≥, ≤) instead of the equals sign (=).
Example: Linear inequality: ( 2x + 3 < 7 )
Solving SAT Algebra Linear Inequalities in One Variable
You can apply the following basic steps to solve SAT Algebra Linear Inequalities in One Variable:
- Isolate the variable on one side of the inequality.
- Perform the same operations on both sides (addition, subtraction, multiplication, division).
- Important: If you multiply or divide by a negative number, reverse the inequality sign.
Example: Solve ( 3x – 5 ≥ 4 ).
- Step 1: Add 5 to both sides: ( 3x ≥ 9 )
- Step 2: Divide by 3: ( x ≥ 3 )
- Graphing the Solution: On a number line, you would represent ( x ≥ 3 ) with a closed circle at 3 shaded to the right.
SAT Algebra Compound Inequalities
These involve two inequalities connected by “and” or “or”. Types:
- Conjunction (And): True if both inequalities are true.
- Disjunction (Or): True if at least one inequality is true.
Example (Conjunction): Solve ( 1 < 2x + 1 < 7 ).
- Break it into two inequalities:
- ( 1 < 2x + 1 )
( 2x + 1 < 7 )
- ( 1 < 2x + 1 )
- Solve both:
- First: ( 0 < 2x -> x > 0 )
- Second: ( 2x < 6 -> x < 3 )
- Combined solution: ( 0 < x < 3 )
- Graphing: Represent this with an open interval on a number line from 0 to 3.
Linear Inequalities in Two Variables
Linear inequality uses two variables, represented in the form ( Ax + By < C ), ( Ax + By > C ), etc.
Example: Linear inequality: ( x + 2y ≤ 4 )
Systems of Linear Inequalities
A set of two or more inequalities that can be graphed on the same coordinate plane.
Example:
( y > x + 1 )
( y < -x + 3 )
SFBS Digital SAT Prep Online Course Program
San Francisco Business School offers a comprehensive Digital SAT Prep Online Course taught by 99th-percentile SAT Instructors and exam experts. The program cracks down each content domain, skills, and knowledge testing point through 1,000+ realistic Digital SAT Exam questions. You will see all the different types of questions that may appear in Digital SAT.
SAT Algebra Exercises for Linear Inequalities in One or Two Variables
To improve your math skills, we do not recommend using a calculator when solving these SAT Math Exercises.
Exercise I. Ryan has $100 and wants to purchase balls. A store sells basketballs and baseballs. Basketballs are $15 each and baseballs are $20 each. If x represents the number of basketballs and y represents the number of baseballs Ryan can purchase, what is the inequality representing this situation?
Exercise II. The maximum value of 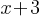 is 13 greater than another number k. What is the inequality for x in terms of k?
is 13 greater than another number k. What is the inequality for x in terms of k?
Exercise III. A High School has students whose height is between 160 cm to 186cm. If h represents the height of a student in this High School, what is the inequality representing the height of a student?
Exercise IV. 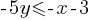
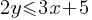
(2, p) is a solution to the given system of inequalities. What is the maximum integer value for p?
💡You can see our Free SAT Math Exercises which has 50 exercises on all SAT Math domains.
SAT Algebra Practice Test
We’ve listed 5 hard SAT Algebra practice test questions below. Note that this test does not resemble the typical question difficulty distribution on a SAT Algebra domain. Instead, we wanted to show you the hardest SAT Math Algebra questions you may see on the SAT.
Besides, since these are the hardest questions for the SAT Algebra, it is very normal that you will spend longer than usual time to solve each question. It is also super normal that you may score lower than your previous SAT Algebra Practice tests in this one. Because a typical Digital SAT Math Practice Test covers easy, medium, and hard questions. However, this one contains only the hardest questions.
Question 1
The equation 9x + 5 =a(x+b), where a and b are constants, has no solutions. Which of the following must be true?
I. a = 9
II. b = 5
III. b ≠ 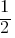
A. None
B. I only
C. I and II only
D. I and III only
Skill and Knowledge Testing Point: Linear equations in one variable
Question 2
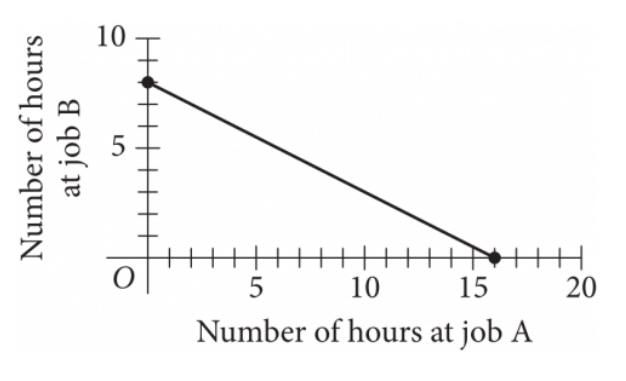
To earn money for college, Avery works two part-time jobs: A and B. She earns $10 per hour working at job A and $20 per hour working at job B. In one week, Avery earned a total of s dollars for working at job B. In one week, Avery earned a total of s dollars for working at the two part-time jobs. The graph above represents all possible combinations of the number of hours Avery could have worked at the two jobs to earn s dollars. What is the value of s ?
A. 128
B. 160
C. 200
D. 320
Skill and Knowledge Testing Point: Linear equations in two variables
Question 3
An object hangs from a spring. The formula 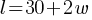 relates the length
relates the length 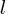 , in centimeters, of the spring to the weight
, in centimeters, of the spring to the weight 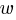 , in newtons, of the object. Which of the following describes the meaning of the 2 in this context?
, in newtons, of the object. Which of the following describes the meaning of the 2 in this context?
A. The length, in centimeters, of the spring with no weight attached
B. The weight, in newtons, of an object that will stretch the spring 30 centimeters
C. The increase in the weight, in newtons, of the object for each one-centimeter increase in the length of the spring
D. The increase in the length, in centimeters, of the spring for each one-newton increase in the weight of the object
Skill and Knowledge Testing Point: Linear functions
SAT Algebra Practice Test – Question 4
Store A sells raspberries for $5.50 per pint and blackberries for $3.00 per pint. Store B sells raspberries for $6.50 per pint and blackberries for $8.00 per pint. A certain purchase of raspberries and blackberries would cost $37.00 at Store A or $66.00 at Store B. How many pints of blackberries are in this purchase?
A. 4
B. 5
C. 8
D. 12
Skill and Knowledge Testing Point: Systems of two linear equations in two variables
Question 5
Ken is working this summer as part of a crew on a farm. He earned $8 per hour for the first 10 hours he worked this week. Because of his performance, his crew leader raised his salary to $10 per hour for the rest of the week. Ken saves 90% of his earnings from each week. What is the least number of hours he must work the rest of the week to save at least $270 for the week?
A. 38
B. 33
C. 22
D. 16
Skill and Knowledge Testing Point: Linear inequalities in one or two variables
SAT Algebra Practice Test Answers and Rationales
We’ve created a comprehensive answers and rationales PDF file for these SAT Algebra Practice questions. If you can fill in your name and email below, we can send it to your email in minutes. Note that, the PDF you will receive will have 19 questions from SAT Math domains. The first 5 questions are answers and rationales for this SAT Algebra Practice Test.
Note that, the email may hit your junk or spam folders, please check your junk and spam folders and if you did not receive it, please email us at support@sanfranciscobs.com.
💡You might be interested in seeing our Digital SAT Math Practice Test. It covers the hardest questions you may see on the SAT Math exam for each skill and knowledge testing point!
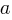 and
and 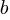 are constants and
are constants and 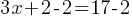 . First, subtract 2 from both sides;
. First, subtract 2 from both sides;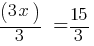 . Then, divide both sides by 3.
. Then, divide both sides by 3.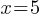
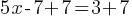 . Add 7 to both sides;
. Add 7 to both sides;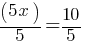 . Divided both sides by 5.
. Divided both sides by 5.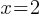
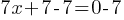 . Subtract 7 from both sides.
. Subtract 7 from both sides.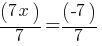 . Divide both sides by 7.
. Divide both sides by 7.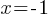
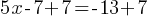 . Add 7 to both sides.
. Add 7 to both sides.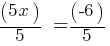 . Divide both sides by 5.
. Divide both sides by 5.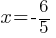
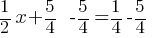 . Subtract
. Subtract 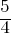 from both sides.
from both sides.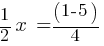 . This equation yields;
. This equation yields;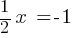 . If we multiply both sides by 2;
. If we multiply both sides by 2;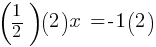 . This yields;
. This yields;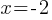 .
.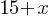 dollars. If Ethan has $35 now;
dollars. If Ethan has $35 now;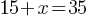 . If we subtract 15 from both sides;
. If we subtract 15 from both sides;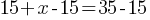 . This yields;
. This yields;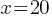 .
.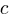 are constants.
are constants.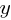 are variables.
are variables.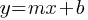 where
where 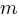 is the slope and
is the slope and 
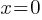 .
.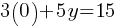 .
.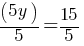 . If we divide both sides by 5;
. If we divide both sides by 5;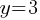 –> (0, 3) is the y-intercept of this graph.
–> (0, 3) is the y-intercept of this graph.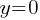 .
.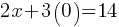 .
.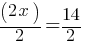 . If we divide both sides by 2;
. If we divide both sides by 2;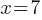 –> (7, 0) is the x-intercept of this graph.
–> (7, 0) is the x-intercept of this graph.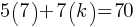 . This yields;
. This yields;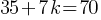 . If we subtract 35 from both sides;
. If we subtract 35 from both sides;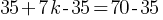 . This yields;
. This yields;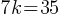 If we divide both sides by 7;
If we divide both sides by 7;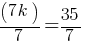 .
.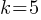
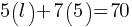 . This yields;
. This yields;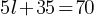 . If we subtract 35 from both sides;
. If we subtract 35 from both sides;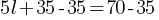 . This yields;
. This yields;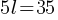 If we divide both sides by 5;
If we divide both sides by 5;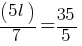 .
.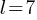
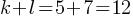
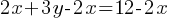 . Subtract
. Subtract 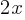 from both sides. This yields;
from both sides. This yields;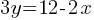 . If we divide both sides by 3;
. If we divide both sides by 3;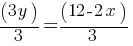 . This equation yields;
. This equation yields;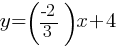 . Now, this equation is in the slope-intercept form y = mx + b.
. Now, this equation is in the slope-intercept form y = mx + b.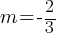 . Since the line k is parallel to this line, it will have the same slope as well.
. Since the line k is parallel to this line, it will have the same slope as well.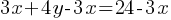 . Subtract
. Subtract 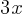 from both sides. This yields;
from both sides. This yields;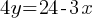 . If we divide both sides by 4;
. If we divide both sides by 4;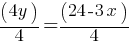 . This equation yields;
. This equation yields;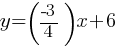 . Now, this equation is in the slope-intercept form y = mx + b.
. Now, this equation is in the slope-intercept form y = mx + b.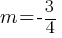 . If line h is perpendicular to this line, the products of the slopes of these two lines will be -1. If we say
. If line h is perpendicular to this line, the products of the slopes of these two lines will be -1. If we say 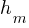 for the slope of line h;
for the slope of line h;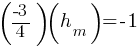 . If we divide both sides by
. If we divide both sides by 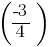 ;
;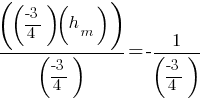 . This yields;
. This yields;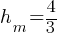
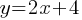
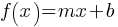 where
where 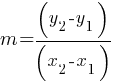

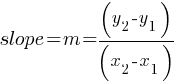 . If we substitute the x and y coordinates of the two points (1, 4) and (3, 10);
. If we substitute the x and y coordinates of the two points (1, 4) and (3, 10);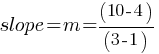 . This yields;
. This yields;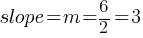 .
.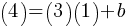 . We substituted (1, 4). x = 1, y = 4. Solving this equation yields;
. We substituted (1, 4). x = 1, y = 4. Solving this equation yields;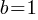 . Now, we can write the equation;
. Now, we can write the equation;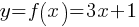
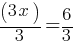 . If we divide both sides by 3;
. If we divide both sides by 3;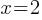 . If we substitute x = 2 in the function equation;
. If we substitute x = 2 in the function equation;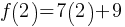 . This yields;
. This yields;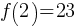
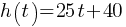
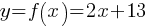 . It is in slope-intercept form of y = mx + b. Therefore;
. It is in slope-intercept form of y = mx + b. Therefore;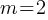 . If we say the slope of y=h(x) is
. If we say the slope of y=h(x) is 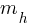 ;
;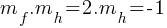 . If we divide both sides by 2;
. If we divide both sides by 2;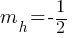 . It’s given that
. It’s given that 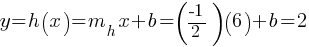 . This yields;
. This yields;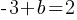 . If we add 3 on both sides;
. If we add 3 on both sides;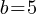 . We found
. We found 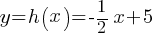
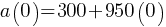 . This yields;
. This yields;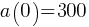 feet.
feet.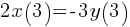 . This yields;
. This yields;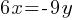 . In the second equation, we can substitute 6x for -9y
. In the second equation, we can substitute 6x for -9y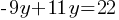 . This yields;
. This yields;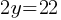 . Dividing both sides by 2;
. Dividing both sides by 2;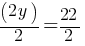 and this yields;
and this yields;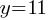 .
.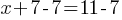 . This yields;
. This yields;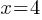 . Now, we can substitute x = 4 in the second equation;
. Now, we can substitute x = 4 in the second equation;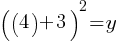 . This yields;
. This yields;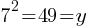
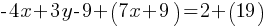 . If we open the parentheses; and combine the like terms;
. If we open the parentheses; and combine the like terms;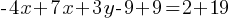 . This yields;
. This yields;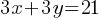 . If we use the common factor of 3 on the left side of the equation;
. If we use the common factor of 3 on the left side of the equation;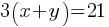 . If we divide both sides by 3; we will find the value of x + y.
. If we divide both sides by 3; we will find the value of x + y.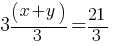 . This yields;
. This yields;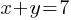
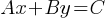 , and
, and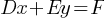
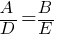 and for these lines to be distinct;
and for these lines to be distinct;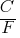 ≠
≠ 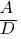 and
and 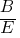
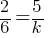 . If we do cross-multiplication;
. If we do cross-multiplication;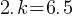 . Dividing both sides by 2 yields;
. Dividing both sides by 2 yields;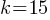 . Note that, when k=15, these two lines are parallel. For them to be distinct;
. Note that, when k=15, these two lines are parallel. For them to be distinct;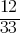 ≠
≠ 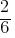 –> This is true. And
–> This is true. And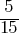 –> this is true as well.
–> this is true as well.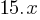 = Total cost of basketballs
= Total cost of basketballs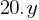 = Total cost of baseballs.
= Total cost of baseballs.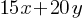 = Total cost of all balls Ryan can purchase.
= Total cost of all balls Ryan can purchase.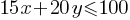
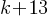 .
.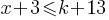 . If we subtract 3 from both sides of the inequality;
. If we subtract 3 from both sides of the inequality;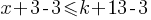 . This yields;
. This yields;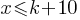
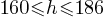
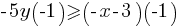 . This yields;
. This yields;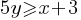 .
.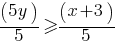 . This yields;
. This yields;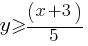 .
.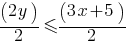 . This yields;
. This yields;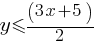 .
.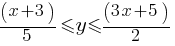 .
.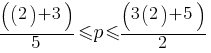 . This yields;
. This yields;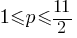 , or
, or 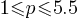
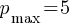 .
.